1.6.12.16. Optimization of a two-parameter function

import numpy as np


# Define the function that we are interested in
def sixhump(x):
    return ((4 - 2.1*x[0]**2 + x[0]**4 / 3.) * x[0]**2 + x[0] * x[1]
            + (-4 + 4*x[1]**2) * x[1] **2)

# Make a grid to evaluate the function (for plotting)
x = np.linspace(-2, 2)
y = np.linspace(-1, 1)
xg, yg = np.meshgrid(x, y)

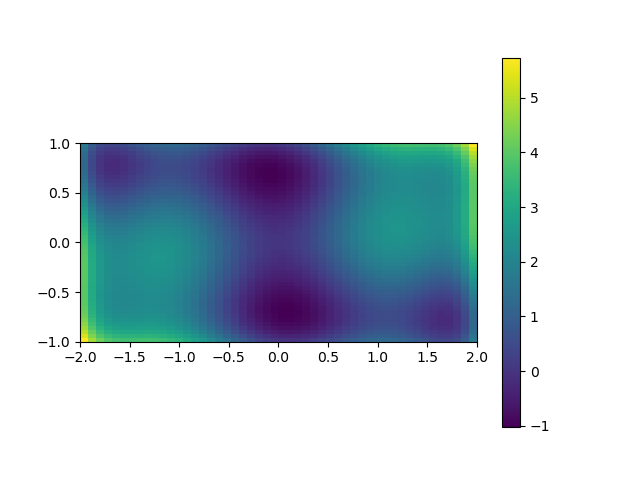
A 2D image plot of the function

Simple visualization in 2D

import matplotlib.pyplot as plt
plt.figure()
plt.imshow(sixhump([xg, yg]), extent=[-2, 2, -1, 1], origin="lower")
plt.colorbar()

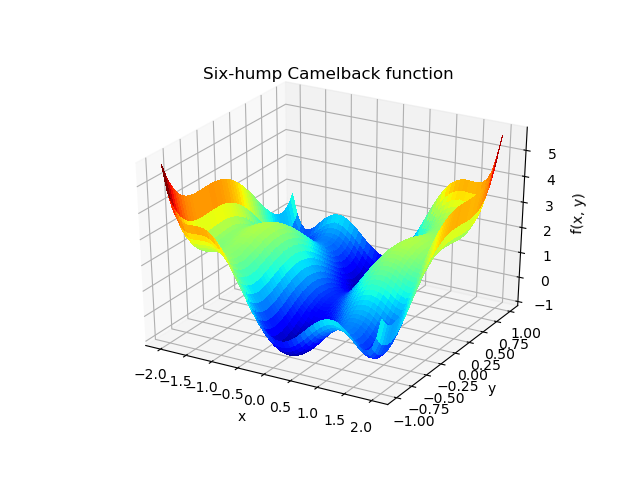
A 3D surface plot of the function

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(xg, yg, sixhump([xg, yg]), rstride=1, cstride=1,
                       cmap=plt.cm.jet, linewidth=0, antialiased=False)

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
ax.set_title('Six-hump Camelback function')

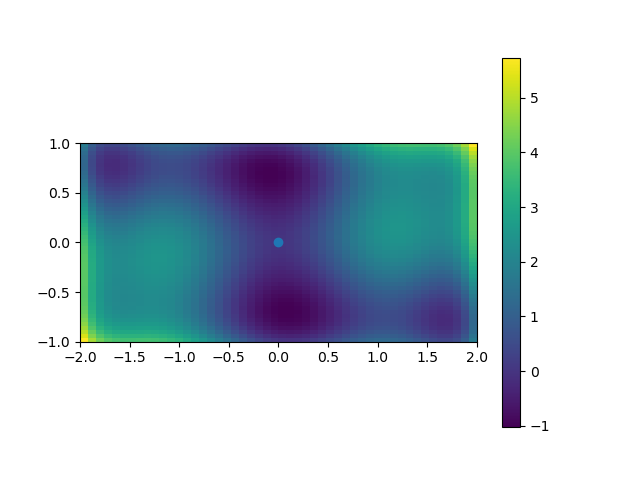
Find the minima

from scipy import optimize

x_min = optimize.minimize(sixhump, x0=[0, 0])

plt.figure()
# Show the function in 2D
plt.imshow(sixhump([xg, yg]), extent=[-2, 2, -1, 1], origin="lower")
plt.colorbar()
# And the minimum that we've found:
plt.scatter(x_min.x[0], x_min.x[1])

plt.show()

Total running time of the script: ( 0 minutes 0.146 seconds)