1.6.12.4. Integrating a simple ODE

Solve the ODE dy/dt = -2y between t = 0..4, with the initial condition y(t=0) = 1.

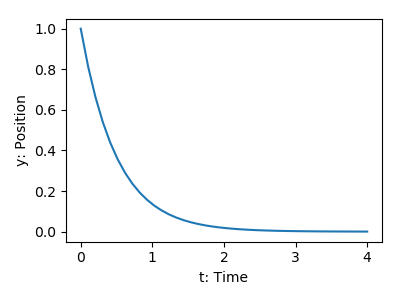
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt

def calc_derivative(ypos, time):
    return -2*ypos

time_vec = np.linspace(0, 4, 40)
yvec = odeint(calc_derivative, 1, time_vec)

plt.figure(figsize=(4, 3))
plt.plot(time_vec, yvec)
plt.xlabel('t: Time')
plt.ylabel('y: Position')
plt.tight_layout()

Total running time of the script: ( 0 minutes 0.034 seconds)