1.6.12.14. Minima and roots of a function

Demos finding minima and roots of a function.

Define the function

import numpy as np

x = np.arange(-10, 10, 0.1)
def f(x):
    return x**2 + 10*np.sin(x)

Find minima

from scipy import optimize

# Global optimization
grid = (-10, 10, 0.1)
xmin_global = optimize.brute(f, (grid, ))
print("Global minima found %s" % xmin_global)

# Constrain optimization
xmin_local = optimize.fminbound(f, 0, 10)
print("Local minimum found %s" % xmin_local)

Out:

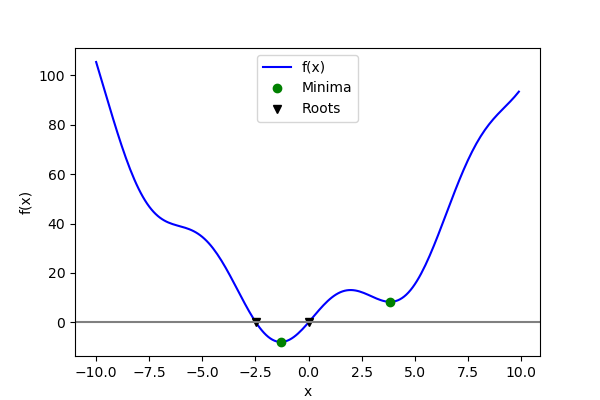
Global minima found [-1.30641113]
Local minimum found 3.8374671194983834

Root finding

root = optimize.root(f, 1)  # our initial guess is 1
print("First root found %s" % root.x)
root2 = optimize.root(f, -2.5)
print("Second root found %s" % root2.x)

Out:

First root found [0.]
Second root found [-2.47948183]

Plot function, minima, and roots

import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6, 4))
ax = fig.add_subplot(111)

# Plot the function
ax.plot(x, f(x), 'b-', label="f(x)")

# Plot the minima
xmins = np.array([xmin_global[0], xmin_local])
ax.plot(xmins, f(xmins), 'go', label="Minima")

# Plot the roots
roots = np.array([root.x, root2.x])
ax.plot(roots, f(roots), 'kv', label="Roots")

# Decorate the figure
ax.legend(loc='best')
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax.axhline(0, color='gray')
plt.show()

Total running time of the script: ( 0 minutes 0.084 seconds)