Image denoising by FFT

Denoise an image (../../../../data/moonlanding.png) by implementing a blur with an FFT.

Implements, via FFT, the following convolution:

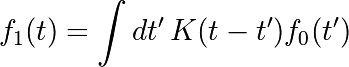
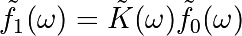
Read and plot the image

import numpy as np
import matplotlib.pyplot as plt

im = plt.imread('../../../../data/moonlanding.png').astype(float)

plt.figure()
plt.imshow(im, plt.cm.gray)
plt.title('Original image')

Compute the 2d FFT of the input image

from scipy import fftpack
im_fft = fftpack.fft2(im)

# Show the results

def plot_spectrum(im_fft):
    from matplotlib.colors import LogNorm
    # A logarithmic colormap
    plt.imshow(np.abs(im_fft), norm=LogNorm(vmin=5))
    plt.colorbar()

plt.figure()
plot_spectrum(im_fft)
plt.title('Fourier transform')

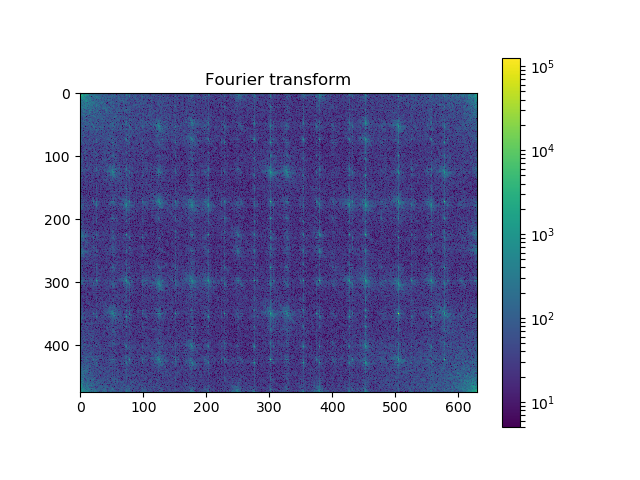
Filter in FFT

# In the lines following, we'll make a copy of the original spectrum and
# truncate coefficients.

# Define the fraction of coefficients (in each direction) we keep
keep_fraction = 0.1

# Call ff a copy of the original transform. Numpy arrays have a copy
# method for this purpose.
im_fft2 = im_fft.copy()

# Set r and c to be the number of rows and columns of the array.
r, c = im_fft2.shape

# Set to zero all rows with indices between r*keep_fraction and
# r*(1-keep_fraction):
im_fft2[int(r*keep_fraction):int(r*(1-keep_fraction))] = 0

# Similarly with the columns:
im_fft2[:, int(c*keep_fraction):int(c*(1-keep_fraction))] = 0

plt.figure()
plot_spectrum(im_fft2)
plt.title('Filtered Spectrum')

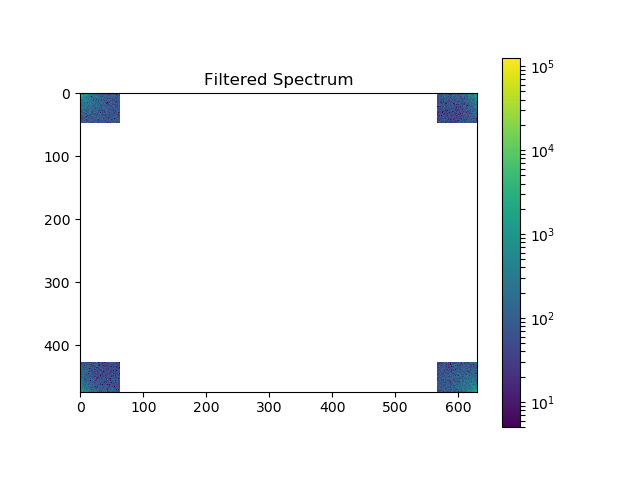
Reconstruct the final image

# Reconstruct the denoised image from the filtered spectrum, keep only the
# real part for display.
im_new = fftpack.ifft2(im_fft2).real

plt.figure()
plt.imshow(im_new, plt.cm.gray)
plt.title('Reconstructed Image')

Easier and better: scipy.ndimage.gaussian_filter()

Implementing filtering directly with FFTs is tricky and time consuming. We can use the Gaussian filter from scipy.ndimage

from scipy import ndimage
im_blur = ndimage.gaussian_filter(im, 4)

plt.figure()
plt.imshow(im_blur, plt.cm.gray)
plt.title('Blurred image')

plt.show()

Total running time of the script: ( 0 minutes 0.211 seconds)