3.6.10.7. Plot variance and regularization in linear models

import numpy as np

# Smaller figures
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = (3, 2)

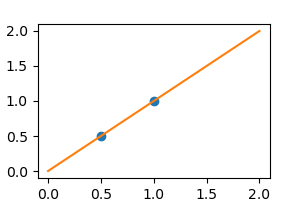
We consider the situation where we have only 2 data point

X = np.c_[ .5, 1].T
y = [.5, 1]
X_test = np.c_[ 0, 2].T

Without noise, as linear regression fits the data perfectly

from sklearn import linear_model
regr = linear_model.LinearRegression()
regr.fit(X, y)
plt.plot(X, y, 'o')
plt.plot(X_test, regr.predict(X_test))

In real life situation, we have noise (e.g. measurement noise) in our data:

np.random.seed(0)
for _ in range(6):
    noisy_X = X + np.random.normal(loc=0, scale=.1, size=X.shape)
    plt.plot(noisy_X, y, 'o')
    regr.fit(noisy_X, y)
    plt.plot(X_test, regr.predict(X_test))

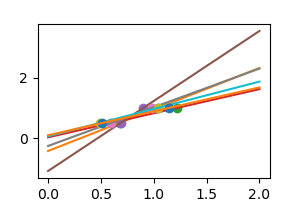
As we can see, our linear model captures and amplifies the noise in the data. It displays a lot of variance.

We can use another linear estimator that uses regularization, the Ridge estimator. This estimator regularizes the coefficients by shrinking them to zero, under the assumption that very high correlations are often spurious. The alpha parameter controls the amount of shrinkage used.

regr = linear_model.Ridge(alpha=.1)
np.random.seed(0)
for _ in range(6):
    noisy_X = X + np.random.normal(loc=0, scale=.1, size=X.shape)
    plt.plot(noisy_X, y, 'o')
    regr.fit(noisy_X, y)
    plt.plot(X_test, regr.predict(X_test))

plt.show()

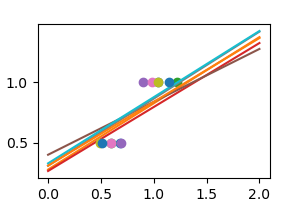
Total running time of the script: ( 0 minutes 0.066 seconds)