3.1.6.3. Analysis of Iris petal and sepal sizes

Ilustrate an analysis on a real dataset:

• Visualizing the data to formulate intuitions
• Fitting of a linear model
• Hypothesis test of the effect of a categorical variable in the presence of a continuous confound

import matplotlib.pyplot as plt

import pandas
from pandas.tools import plotting

from statsmodels.formula.api import ols

# Load the data
data = pandas.read_csv('iris.csv')

Plot a scatter matrix

# Express the names as categories
categories = pandas.Categorical(data['name'])

# The parameter 'c' is passed to plt.scatter and will control the color
plotting.scatter_matrix(data, c=categories.codes, marker='o')

fig = plt.gcf()
fig.suptitle("blue: setosa, green: versicolor, red: virginica", size=13)

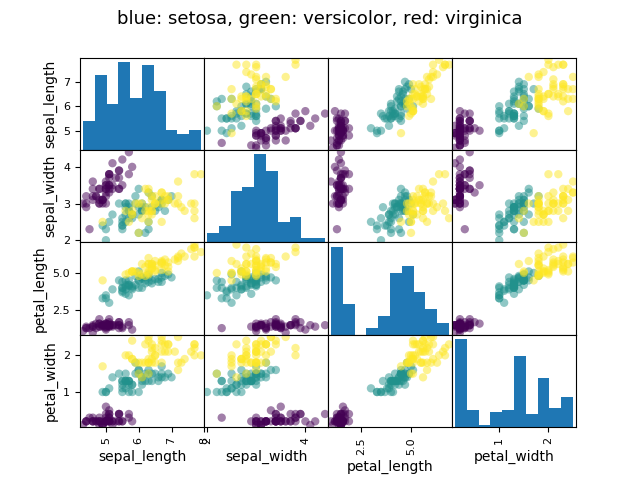
Statistical analysis

# Let us try to explain the sepal length as a function of the petal
# width and the category of iris

model = ols('sepal_width ~ name + petal_length', data).fit()
print(model.summary())

# Now formulate a "contrast", to test if the offset for versicolor and
# virginica are identical

print('Testing the difference between effect of versicolor and virginica')
print(model.f_test([0, 1, -1, 0]))
plt.show()

Out:

OLS Regression Results
==============================================================================
Dep. Variable:            sepal_width   R-squared:                       0.478
Model:                            OLS   Adj. R-squared:                  0.468
Method:                 Least Squares   F-statistic:                     44.63
Date:                Thu, 18 Aug 2022   Prob (F-statistic):           1.58e-20
Time:                        10:40:00   Log-Likelihood:                -38.185
No. Observations:                 150   AIC:                             84.37
Df Residuals:                     146   BIC:                             96.41
Df Model:                           3
Covariance Type:            nonrobust
======================================================================================
                         coef    std err          t      P>|t|      [0.025      0.975]
--------------------------------------------------------------------------------------
Intercept              2.9813      0.099     29.989      0.000       2.785       3.178
name[T.versicolor]    -1.4821      0.181     -8.190      0.000      -1.840      -1.124
name[T.virginica]     -1.6635      0.256     -6.502      0.000      -2.169      -1.158
petal_length           0.2983      0.061      4.920      0.000       0.178       0.418
==============================================================================
Omnibus:                        2.868   Durbin-Watson:                   1.753
Prob(Omnibus):                  0.238   Jarque-Bera (JB):                2.885
Skew:                          -0.082   Prob(JB):                        0.236
Kurtosis:                       3.659   Cond. No.                         54.0
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Testing the difference between effect of versicolor and virginica
<F test: F=array([[3.24533535]]), p=0.07369058781700064, df_denom=146, df_num=1>

Total running time of the script: ( 0 minutes 0.387 seconds)