2.6. Image manipulation and processing using Numpy and Scipy

Authors: Emmanuelle Gouillart, Gaël Varoquaux

This section addresses basic image manipulation and processing using the core scientific modules NumPy and SciPy. Some of the operations covered by this tutorial may be useful for other kinds of multidimensional array processing than image processing. In particular, the submodule scipy.ndimage provides functions operating on n-dimensional NumPy arrays.

See also

For more advanced image processing and image-specific routines, see the tutorial Scikit-image: image processing, dedicated to the skimage module.

Image = 2-D numerical array

(or 3-D: CT, MRI, 2D + time; 4-D, …)

Here, image == Numpy array np.array

Tools used in this tutorial:

  • numpy: basic array manipulation

  • scipy: scipy.ndimage submodule dedicated to image processing (n-dimensional images). See the documentation:

    >>> from scipy import ndimage

Common tasks in image processing:

  • Input/Output, displaying images
  • Basic manipulations: cropping, flipping, rotating, …
  • Image filtering: denoising, sharpening
  • Image segmentation: labeling pixels corresponding to different objects
  • Classification
  • Feature extraction
  • Registration
  • …

2.6.1. Opening and writing to image files

Writing an array to a file:

from scipy import misc

import imageio

f = misc.face()

imageio.imsave('face.png', f) # uses the Image module (PIL)



import matplotlib.pyplot as plt

plt.imshow(f)

plt.show()
../../_images/face.png

Creating a numpy array from an image file:

>>> from scipy import misc

>>> import imageio

>>> face = misc.face()

>>> imageio.imsave('face.png', face) # First we need to create the PNG file



>>> face = imageio.imread('face.png')

>>> type(face)      

<class 'imageio.core.util.Array'>

>>> face.shape, face.dtype

((768, 1024, 3), dtype('uint8'))

dtype is uint8 for 8-bit images (0-255)

Opening raw files (camera, 3-D images)

>>> face.tofile('face.raw') # Create raw file

>>> face_from_raw = np.fromfile('face.raw', dtype=np.uint8)

>>> face_from_raw.shape

(2359296,)

>>> face_from_raw.shape = (768, 1024, 3)

Need to know the shape and dtype of the image (how to separate data bytes).

For large data, use np.memmap for memory mapping:

>>> face_memmap = np.memmap('face.raw', dtype=np.uint8, shape=(768, 1024, 3))

(data are read from the file, and not loaded into memory)

Working on a list of image files

>>> for i in range(10):

...     im = np.random.randint(0, 256, 10000).reshape((100, 100))

...     imageio.imsave('random_%02d.png' % i, im)

>>> from glob import glob

>>> filelist = glob('random*.png')

>>> filelist.sort()

2.6.2. Displaying images

Use matplotlib and imshow to display an image inside a matplotlib figure:

>>> f = misc.face(gray=True)  # retrieve a grayscale image

>>> import matplotlib.pyplot as plt

>>> plt.imshow(f, cmap=plt.cm.gray)        

<matplotlib.image.AxesImage object at 0x...>

Increase contrast by setting min and max values:

>>> plt.imshow(f, cmap=plt.cm.gray, vmin=30, vmax=200)        

<matplotlib.image.AxesImage object at 0x...>

>>> # Remove axes and ticks

>>> plt.axis('off')

(-0.5, 1023.5, 767.5, -0.5)

Draw contour lines:

>>> plt.contour(f, [50, 200])        

<matplotlib.contour.QuadContourSet ...>
../../_images/sphx_glr_plot_display_face_001.png

[Python source code]

For smooth intensity variations, use interpolation='bilinear'. For fine inspection of intensity variations, use interpolation='nearest':

>>> plt.imshow(f[320:340, 510:530], cmap=plt.cm.gray, interpolation='bilinear')        

<matplotlib.image.AxesImage object at 0x...>

>>> plt.imshow(f[320:340, 510:530], cmap=plt.cm.gray, interpolation='nearest')        

<matplotlib.image.AxesImage object at 0x...>
../../_images/sphx_glr_plot_interpolation_face_001.png

[Python source code]

See also

More interpolation methods are in Matplotlib’s examples.

See also

3-D visualization: Mayavi

See 3D plotting with Mayavi.

  • Image plane widgets
  • Isosurfaces
  • …
../../_images/decorations.png

2.6.3. Basic manipulations

Images are arrays: use the whole numpy machinery.

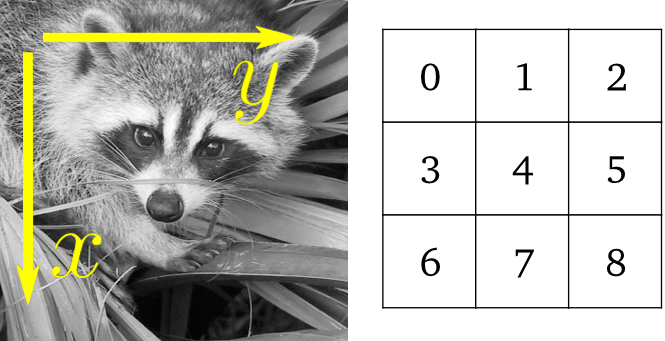
../../_images/axis_convention.png 
>>> face = misc.face(gray=True)

>>> face[0, 40]

127

>>> # Slicing

>>> face[10:13, 20:23]

array([[141, 153, 145],

       [133, 134, 125],

       [ 96,  92,  94]], dtype=uint8)

>>> face[100:120] = 255

>>>

>>> lx, ly = face.shape

>>> X, Y = np.ogrid[0:lx, 0:ly]

>>> mask = (X - lx / 2) ** 2 + (Y - ly / 2) ** 2 > lx * ly / 4

>>> # Masks

>>> face[mask] = 0

>>> # Fancy indexing

>>> face[range(400), range(400)] = 255
../../_images/sphx_glr_plot_numpy_array_001.png

[Python source code]

2.6.3.1. Statistical information

>>> face = misc.face(gray=True)

>>> face.mean()

113.48026784261067

>>> face.max(), face.min()

(250, 0)

np.histogram

Exercise

  • Open as an array the scikit-image logo (http://scikit-image.org/_static/img/logo.png), or an image that you have on your computer.
  • Crop a meaningful part of the image, for example the python circle in the logo.
  • Display the image array using matplotlib. Change the interpolation method and zoom to see the difference.
  • Transform your image to greyscale
  • Increase the contrast of the image by changing its minimum and maximum values. Optional: use scipy.stats.scoreatpercentile (read the docstring!) to saturate 5% of the darkest pixels and 5% of the lightest pixels.
  • Save the array to two different file formats (png, jpg, tiff)
../../_images/scikit_image_logo.png

2.6.3.2. Geometrical transformations

>>> face = misc.face(gray=True)

>>> lx, ly = face.shape

>>> # Cropping

>>> crop_face = face[lx // 4: - lx // 4, ly // 4: - ly // 4]

>>> # up <-> down flip

>>> flip_ud_face = np.flipud(face)

>>> # rotation

>>> rotate_face = ndimage.rotate(face, 45)

>>> rotate_face_noreshape = ndimage.rotate(face, 45, reshape=False)
../../_images/sphx_glr_plot_geom_face_001.png

[Python source code]

2.6.4. Image filtering

Local filters: replace the value of pixels by a function of the values of neighboring pixels.

Neighbourhood: square (choose size), disk, or more complicated structuring element.

../../_images/kernels.png

2.6.4.1. Blurring/smoothing

Gaussian filter from scipy.ndimage:

>>> from scipy import misc

>>> face = misc.face(gray=True)

>>> blurred_face = ndimage.gaussian_filter(face, sigma=3)

>>> very_blurred = ndimage.gaussian_filter(face, sigma=5)

Uniform filter

>>> local_mean = ndimage.uniform_filter(face, size=11)
../../_images/sphx_glr_plot_blur_001.png

[Python source code]

2.6.4.2. Sharpening

Sharpen a blurred image:

>>> from scipy import misc

>>> face = misc.face(gray=True).astype(float)

>>> blurred_f = ndimage.gaussian_filter(face, 3)

increase the weight of edges by adding an approximation of the Laplacian:

>>> filter_blurred_f = ndimage.gaussian_filter(blurred_f, 1)

>>> alpha = 30

>>> sharpened = blurred_f + alpha * (blurred_f - filter_blurred_f)
../../_images/sphx_glr_plot_sharpen_001.png

[Python source code]

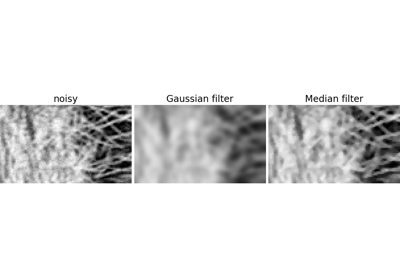
2.6.4.3. Denoising

Noisy face:

>>> from scipy import misc

>>> f = misc.face(gray=True)

>>> f = f[230:290, 220:320]

>>> noisy = f + 0.4 * f.std() * np.random.random(f.shape)

A Gaussian filter smoothes the noise out… and the edges as well:

>>> gauss_denoised = ndimage.gaussian_filter(noisy, 2)

Most local linear isotropic filters blur the image (ndimage.uniform_filter)

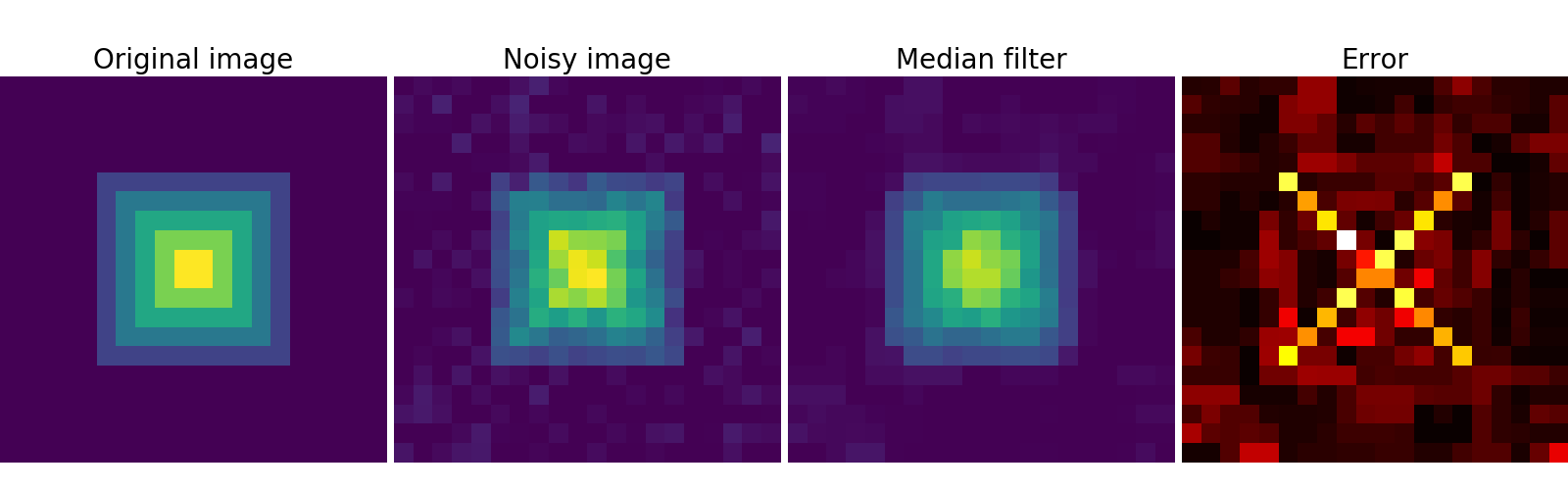
A median filter preserves better the edges:

>>> med_denoised = ndimage.median_filter(noisy, 3)
../../_images/sphx_glr_plot_face_denoise_001.png

[Python source code]

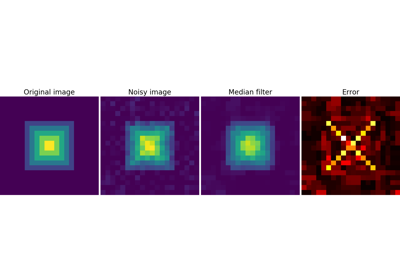
Median filter: better result for straight boundaries (low curvature):

>>> im = np.zeros((20, 20))

>>> im[5:-5, 5:-5] = 1

>>> im = ndimage.distance_transform_bf(im)

>>> im_noise = im + 0.2 * np.random.randn(*im.shape)

>>> im_med = ndimage.median_filter(im_noise, 3)
../../_images/sphx_glr_plot_denoising_001.png

[Python source code]

Other rank filter: ndimage.maximum_filter, ndimage.percentile_filter

Other local non-linear filters: Wiener (scipy.signal.wiener), etc.

Non-local filters

Exercise: denoising

  • Create a binary image (of 0s and 1s) with several objects (circles, ellipses, squares, or random shapes).
  • Add some noise (e.g., 20% of noise)
  • Try two different denoising methods for denoising the image: gaussian filtering and median filtering.
  • Compare the histograms of the two different denoised images. Which one is the closest to the histogram of the original (noise-free) image?

See also

More denoising filters are available in skimage.denoising, see the Scikit-image: image processing tutorial.

2.6.4.4. Mathematical morphology

See wikipedia for a definition of mathematical morphology.

Probe an image with a simple shape (a structuring element), and modify this image according to how the shape locally fits or misses the image.

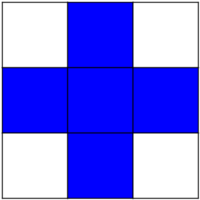
Structuring element:

>>> el = ndimage.generate_binary_structure(2, 1)

>>> el

array([[False,  True, False],

       [ True,  True,  True],

       [False,  True, False]])

>>> el.astype(np.int)

array([[0, 1, 0],

       [1, 1, 1],

       [0, 1, 0]])
../../_images/diamond_kernel.png

Erosion = minimum filter. Replace the value of a pixel by the minimal value covered by the structuring element.:

>>> a = np.zeros((7,7), dtype=np.int)

>>> a[1:6, 2:5] = 1

>>> a

array([[0, 0, 0, 0, 0, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 1, 1, 1, 0, 0],

       [0, 0, 0, 0, 0, 0, 0]])

>>> ndimage.binary_erosion(a).astype(a.dtype)

array([[0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 1, 0, 0, 0],

       [0, 0, 0, 1, 0, 0, 0],

       [0, 0, 0, 1, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0]])

>>> #Erosion removes objects smaller than the structure

>>> ndimage.binary_erosion(a, structure=np.ones((5,5))).astype(a.dtype)

array([[0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0],

       [0, 0, 0, 0, 0, 0, 0]])
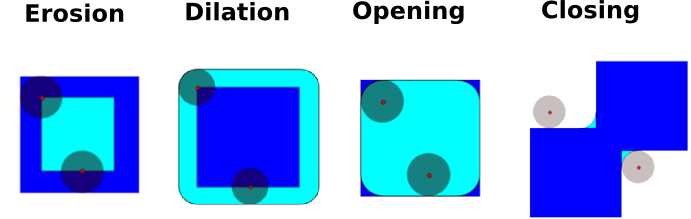
../../_images/morpho_mat.png

Dilation: maximum filter:

>>> a = np.zeros((5, 5))

>>> a[2, 2] = 1

>>> a

array([[0.,  0.,  0.,  0.,  0.],

       [0.,  0.,  0.,  0.,  0.],

       [0.,  0.,  1.,  0.,  0.],

       [0.,  0.,  0.,  0.,  0.],

       [0.,  0.,  0.,  0.,  0.]])

>>> ndimage.binary_dilation(a).astype(a.dtype)

array([[0.,  0.,  0.,  0.,  0.],

       [0.,  0.,  1.,  0.,  0.],

       [0.,  1.,  1.,  1.,  0.],

       [0.,  0.,  1.,  0.,  0.],

       [0.,  0.,  0.,  0.,  0.]])

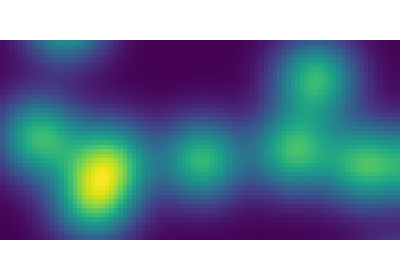
Also works for grey-valued images:

>>> np.random.seed(2)

>>> im = np.zeros((64, 64))

>>> x, y = (63*np.random.random((2, 8))).astype(np.int)

>>> im[x, y] = np.arange(8)



>>> bigger_points = ndimage.grey_dilation(im, size=(5, 5), structure=np.ones((5, 5)))



>>> square = np.zeros((16, 16))

>>> square[4:-4, 4:-4] = 1

>>> dist = ndimage.distance_transform_bf(square)

>>> dilate_dist = ndimage.grey_dilation(dist, size=(3, 3), \

...         structure=np.ones((3, 3)))
../../_images/sphx_glr_plot_greyscale_dilation_001.png

[Python source code]

Opening: erosion + dilation:

>>> a = np.zeros((5,5), dtype=np.int)

>>> a[1:4, 1:4] = 1; a[4, 4] = 1

>>> a

array([[0, 0, 0, 0, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 0, 0, 0, 1]])

>>> # Opening removes small objects

>>> ndimage.binary_opening(a, structure=np.ones((3,3))).astype(np.int)

array([[0, 0, 0, 0, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 1, 1, 1, 0],

       [0, 0, 0, 0, 0]])

>>> # Opening can also smooth corners

>>> ndimage.binary_opening(a).astype(np.int)

array([[0, 0, 0, 0, 0],

       [0, 0, 1, 0, 0],

       [0, 1, 1, 1, 0],

       [0, 0, 1, 0, 0],

       [0, 0, 0, 0, 0]])

Application: remove noise:

>>> square = np.zeros((32, 32))

>>> square[10:-10, 10:-10] = 1

>>> np.random.seed(2)

>>> x, y = (32*np.random.random((2, 20))).astype(np.int)

>>> square[x, y] = 1



>>> open_square = ndimage.binary_opening(square)



>>> eroded_square = ndimage.binary_erosion(square)

>>> reconstruction = ndimage.binary_propagation(eroded_square, mask=square)
../../_images/sphx_glr_plot_propagation_001.png

[Python source code]

Closing: dilation + erosion

Many other mathematical morphology operations: hit and miss transform, tophat, etc.

2.6.5. Feature extraction

2.6.5.1. Edge detection

Synthetic data:

>>> im = np.zeros((256, 256))

>>> im[64:-64, 64:-64] = 1

>>>

>>> im = ndimage.rotate(im, 15, mode='constant')

>>> im = ndimage.gaussian_filter(im, 8)

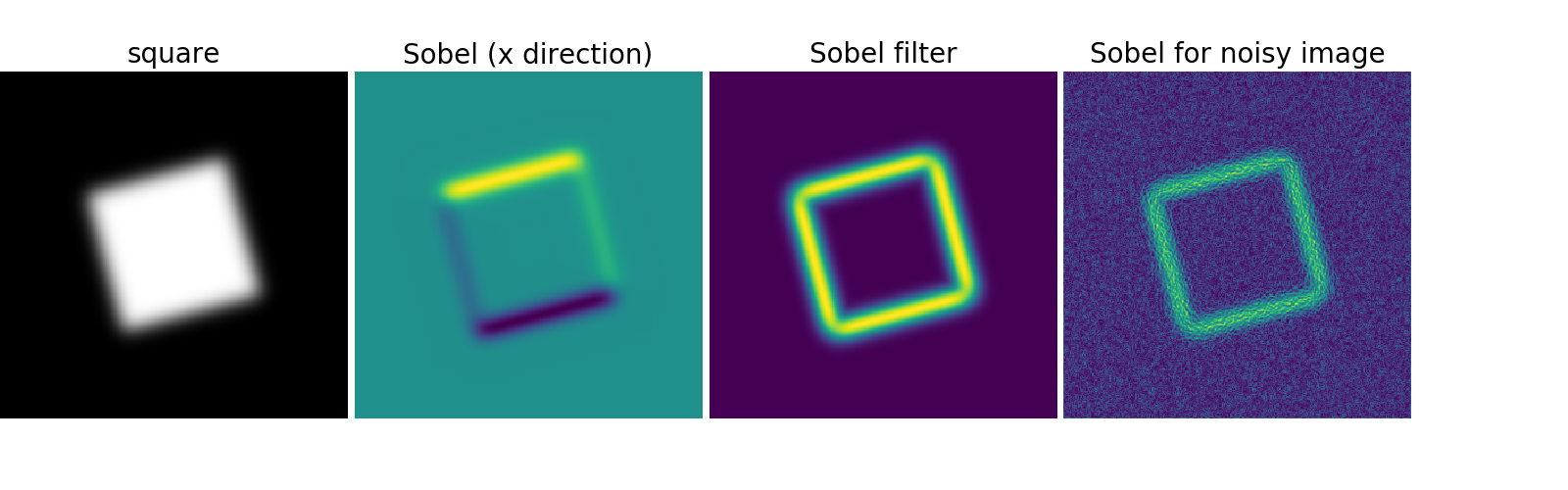
Use a gradient operator (Sobel) to find high intensity variations:

>>> sx = ndimage.sobel(im, axis=0, mode='constant')

>>> sy = ndimage.sobel(im, axis=1, mode='constant')

>>> sob = np.hypot(sx, sy)
../../_images/sphx_glr_plot_find_edges_001.png

[Python source code]

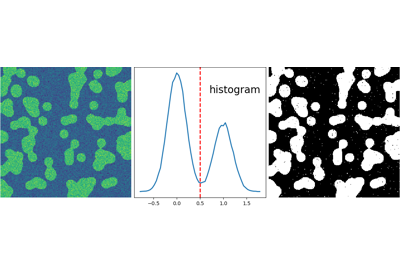
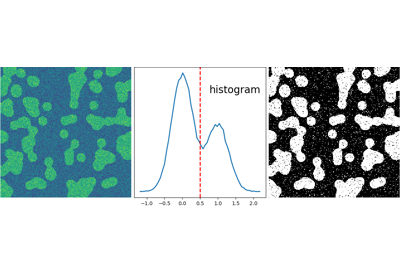
2.6.5.2. Segmentation

  • Histogram-based segmentation (no spatial information)
>>> n = 10

>>> l = 256

>>> im = np.zeros((l, l))

>>> np.random.seed(1)

>>> points = l*np.random.random((2, n**2))

>>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1

>>> im = ndimage.gaussian_filter(im, sigma=l/(4.*n))



>>> mask = (im > im.mean()).astype(np.float)

>>> mask += 0.1 * im

>>> img = mask + 0.2*np.random.randn(*mask.shape)



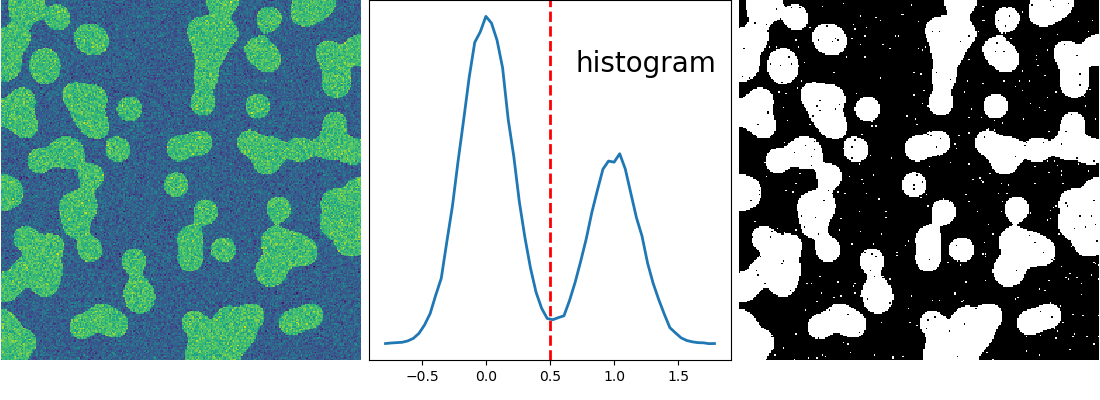
>>> hist, bin_edges = np.histogram(img, bins=60)

>>> bin_centers = 0.5*(bin_edges[:-1] + bin_edges[1:])



>>> binary_img = img > 0.5
../../_images/sphx_glr_plot_histo_segmentation_001.png

[Python source code]

Use mathematical morphology to clean up the result:

>>> # Remove small white regions

>>> open_img = ndimage.binary_opening(binary_img)

>>> # Remove small black hole

>>> close_img = ndimage.binary_closing(open_img)
../../_images/sphx_glr_plot_clean_morpho_001.png

[Python source code]

Exercise

Check that reconstruction operations (erosion + propagation) produce a better result than opening/closing:

>>> eroded_img = ndimage.binary_erosion(binary_img)

>>> reconstruct_img = ndimage.binary_propagation(eroded_img, mask=binary_img)

>>> tmp = np.logical_not(reconstruct_img)

>>> eroded_tmp = ndimage.binary_erosion(tmp)

>>> reconstruct_final = np.logical_not(ndimage.binary_propagation(eroded_tmp, mask=tmp))

>>> np.abs(mask - close_img).mean() 

0.00727836...

>>> np.abs(mask - reconstruct_final).mean() 

0.00059502...

Exercise

Check how a first denoising step (e.g. with a median filter) modifies the histogram, and check that the resulting histogram-based segmentation is more accurate.

See also

More advanced segmentation algorithms are found in the scikit-image: see Scikit-image: image processing.

See also

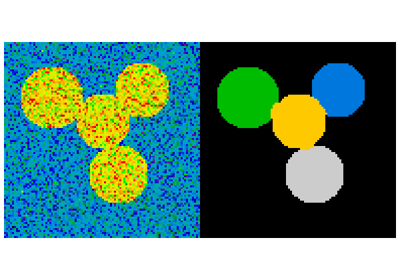
Other Scientific Packages provide algorithms that can be useful for image processing. In this example, we use the spectral clustering function of the scikit-learn in order to segment glued objects.

>>> from sklearn.feature_extraction import image

>>> from sklearn.cluster import spectral_clustering



>>> l = 100

>>> x, y = np.indices((l, l))



>>> center1 = (28, 24)

>>> center2 = (40, 50)

>>> center3 = (67, 58)

>>> center4 = (24, 70)

>>> radius1, radius2, radius3, radius4 = 16, 14, 15, 14



>>> circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2

>>> circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2

>>> circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2

>>> circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2



>>> # 4 circles

>>> img = circle1 + circle2 + circle3 + circle4

>>> mask = img.astype(bool)

>>> img = img.astype(float)



>>> img += 1 + 0.2*np.random.randn(*img.shape)

>>> # Convert the image into a graph with the value of the gradient on

>>> # the edges.

>>> graph = image.img_to_graph(img, mask=mask)



>>> # Take a decreasing function of the gradient: we take it weakly

>>> # dependant from the gradient the segmentation is close to a voronoi

>>> graph.data = np.exp(-graph.data/graph.data.std())



>>> labels = spectral_clustering(graph, n_clusters=4, eigen_solver='arpack')

>>> label_im = -np.ones(mask.shape)

>>> label_im[mask] = labels
../../_images/image_spectral_clustering.png

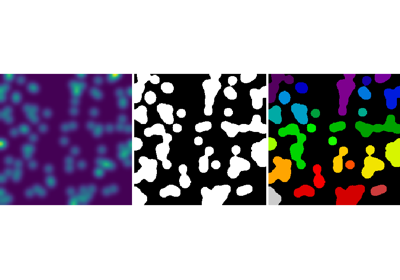
2.6.6. Measuring objects properties: ndimage.measurements

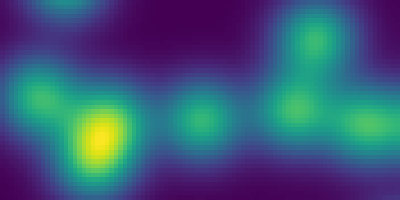
Synthetic data:

>>> n = 10

>>> l = 256

>>> im = np.zeros((l, l))

>>> points = l*np.random.random((2, n**2))

>>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1

>>> im = ndimage.gaussian_filter(im, sigma=l/(4.*n))

>>> mask = im > im.mean()
  • Analysis of connected components

Label connected components: ndimage.label:

>>> label_im, nb_labels = ndimage.label(mask)

>>> nb_labels # how many regions?

29

>>> plt.imshow(label_im)        

<matplotlib.image.AxesImage object at 0x...>
../../_images/sphx_glr_plot_synthetic_data_001.png

[Python source code]

Compute size, mean_value, etc. of each region:

>>> sizes = ndimage.sum(mask, label_im, range(nb_labels + 1))

>>> mean_vals = ndimage.sum(im, label_im, range(1, nb_labels + 1))

Clean up small connect components:

>>> mask_size = sizes < 1000

>>> remove_pixel = mask_size[label_im]

>>> remove_pixel.shape

(256, 256)

>>> label_im[remove_pixel] = 0

>>> plt.imshow(label_im)        

<matplotlib.image.AxesImage object at 0x...>

Now reassign labels with np.searchsorted:

>>> labels = np.unique(label_im)

>>> label_im = np.searchsorted(labels, label_im)
../../_images/sphx_glr_plot_measure_data_001.png

[Python source code]

Find region of interest enclosing object:

>>> slice_x, slice_y = ndimage.find_objects(label_im==4)[0]

>>> roi = im[slice_x, slice_y]

>>> plt.imshow(roi)     

<matplotlib.image.AxesImage object at 0x...>
../../_images/sphx_glr_plot_find_object_001.png

[Python source code]

Other spatial measures: ndimage.center_of_mass, ndimage.maximum_position, etc.

Can be used outside the limited scope of segmentation applications.

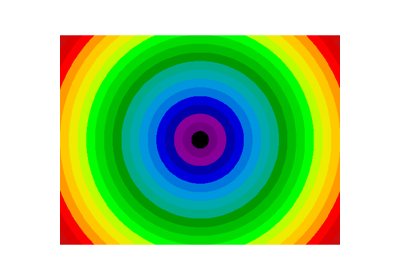
Example: block mean:

>>> from scipy import misc

>>> f = misc.face(gray=True)

>>> sx, sy = f.shape

>>> X, Y = np.ogrid[0:sx, 0:sy]

>>> regions = (sy//6) * (X//4) + (Y//6)  # note that we use broadcasting

>>> block_mean = ndimage.mean(f, labels=regions, index=np.arange(1,

...     regions.max() +1))

>>> block_mean.shape = (sx // 4, sy // 6)
../../_images/sphx_glr_plot_block_mean_001.png

[Python source code]

When regions are regular blocks, it is more efficient to use stride tricks (Example: fake dimensions with strides).

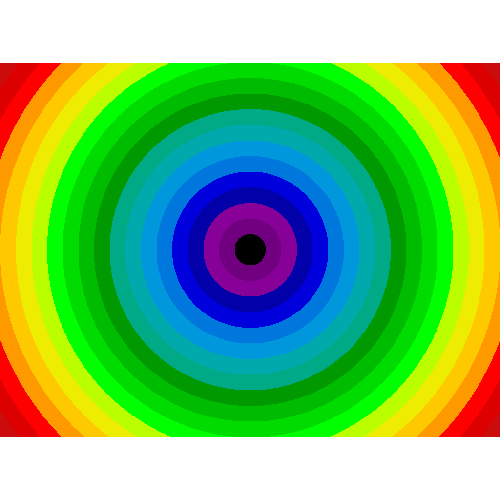
Non-regularly-spaced blocks: radial mean:

>>> sx, sy = f.shape

>>> X, Y = np.ogrid[0:sx, 0:sy]

>>> r = np.hypot(X - sx/2, Y - sy/2)

>>> rbin = (20* r/r.max()).astype(np.int)

>>> radial_mean = ndimage.mean(f, labels=rbin, index=np.arange(1, rbin.max() +1))
../../_images/sphx_glr_plot_radial_mean_001.png

[Python source code]

  • Other measures

Correlation function, Fourier/wavelet spectrum, etc.

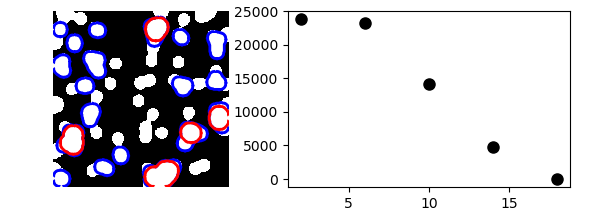
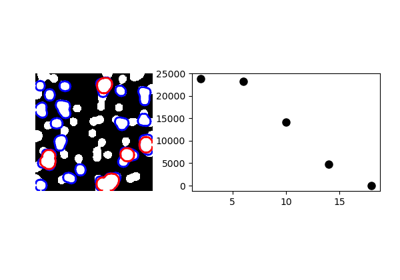
One example with mathematical morphology: granulometry

>>> def disk_structure(n):

...     struct = np.zeros((2 * n + 1, 2 * n + 1))

...     x, y = np.indices((2 * n + 1, 2 * n + 1))

...     mask = (x - n)**2 + (y - n)**2 <= n**2

...     struct[mask] = 1

...     return struct.astype(np.bool)

...

>>>

>>> def granulometry(data, sizes=None):

...     s = max(data.shape)

...     if sizes is None:

...         sizes = range(1, s/2, 2)

...     granulo = [ndimage.binary_opening(data, \

...         structure=disk_structure(n)).sum() for n in sizes]

...     return granulo

...

>>>

>>> np.random.seed(1)

>>> n = 10

>>> l = 256

>>> im = np.zeros((l, l))

>>> points = l*np.random.random((2, n**2))

>>> im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1

>>> im = ndimage.gaussian_filter(im, sigma=l/(4.*n))

>>>

>>> mask = im > im.mean()

>>>

>>> granulo = granulometry(mask, sizes=np.arange(2, 19, 4))
../../_images/sphx_glr_plot_granulo_001.png

[Python source code]