1.4.2. Numerical operations on arrays¶
Section contents
1.4.2.1. Elementwise operations¶
Basic operations¶
With scalars:
>>> a = np.array([1, 2, 3, 4])
>>> a + 1
array([2, 3, 4, 5])
>>> 2**a
array([ 2, 4, 8, 16])
All arithmetic operates elementwise:
>>> b = np.ones(4) + 1
>>> a - b
array([-1., 0., 1., 2.])
>>> a * b
array([2., 4., 6., 8.])
>>> j = np.arange(5)
>>> 2**(j + 1) - j
array([ 2, 3, 6, 13, 28])
These operations are of course much faster than if you did them in pure python:
>>> a = np.arange(10000)
>>> %timeit a + 1
10000 loops, best of 3: 24.3 us per loop
>>> l = range(10000)
>>> %timeit [i+1 for i in l]
1000 loops, best of 3: 861 us per loop
Warning
Array multiplication is not matrix multiplication:
>>> c = np.ones((3, 3))
>>> c * c # NOT matrix multiplication!
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
Note
Matrix multiplication:
>>> c.dot(c)
array([[3., 3., 3.],
[3., 3., 3.],
[3., 3., 3.]])
Exercise: Elementwise operations
- Try simple arithmetic elementwise operations: add even elements with odd elements
- Time them against their pure python counterparts using
%timeit.- Generate:
[2**0, 2**1, 2**2, 2**3, 2**4]a_j = 2^(3*j) - j
Other operations¶
Comparisons:
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([4, 2, 2, 4])
>>> a == b
array([False, True, False, True])
>>> a > b
array([False, False, True, False])
Tip
Array-wise comparisons:
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([4, 2, 2, 4])
>>> c = np.array([1, 2, 3, 4])
>>> np.array_equal(a, b)
False
>>> np.array_equal(a, c)
True
Logical operations:
>>> a = np.array([1, 1, 0, 0], dtype=bool)
>>> b = np.array([1, 0, 1, 0], dtype=bool)
>>> np.logical_or(a, b)
array([ True, True, True, False])
>>> np.logical_and(a, b)
array([ True, False, False, False])
Transcendental functions:
>>> a = np.arange(5)
>>> np.sin(a)
array([ 0. , 0.84147098, 0.90929743, 0.14112001, -0.7568025 ])
>>> np.log(a)
array([ -inf, 0. , 0.69314718, 1.09861229, 1.38629436])
>>> np.exp(a)
array([ 1. , 2.71828183, 7.3890561 , 20.08553692, 54.59815003])
Shape mismatches
>>> a = np.arange(4)
>>> a + np.array([1, 2])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (4) (2)
Broadcasting? We’ll return to that later.
Transposition:
>>> a = np.triu(np.ones((3, 3)), 1) # see help(np.triu)
>>> a
array([[0., 1., 1.],
[0., 0., 1.],
[0., 0., 0.]])
>>> a.T
array([[0., 0., 0.],
[1., 0., 0.],
[1., 1., 0.]])
Note
The transposition is a view
The transpose returns a view of the original array:
>>> a = np.arange(9).reshape(3, 3)
>>> a.T[0, 2] = 999
>>> a.T
array([[ 0, 3, 999],
[ 1, 4, 7],
[ 2, 5, 8]])
>>> a
array([[ 0, 1, 2],
[ 3, 4, 5],
[999, 7, 8]])
Note
Linear algebra
The sub-module numpy.linalg implements basic linear algebra, such as
solving linear systems, singular value decomposition, etc. However, it is
not guaranteed to be compiled using efficient routines, and thus we
recommend the use of scipy.linalg, as detailed in section
Linear algebra operations: scipy.linalg
Exercise other operations
- Look at the help for
np.allclose. When might this be useful?- Look at the help for
np.triuandnp.tril.
1.4.2.2. Basic reductions¶
Computing sums¶
>>> x = np.array([1, 2, 3, 4])
>>> np.sum(x)
10
>>> x.sum()
10
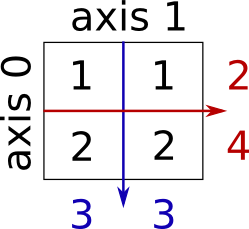
Sum by rows and by columns:
>>> x = np.array([[1, 1], [2, 2]])
>>> x
array([[1, 1],
[2, 2]])
>>> x.sum(axis=0) # columns (first dimension)
array([3, 3])
>>> x[:, 0].sum(), x[:, 1].sum()
(3, 3)
>>> x.sum(axis=1) # rows (second dimension)
array([2, 4])
>>> x[0, :].sum(), x[1, :].sum()
(2, 4)
Tip
Same idea in higher dimensions:
>>> x = np.random.rand(2, 2, 2)
>>> x.sum(axis=2)[0, 1]
1.14764...
>>> x[0, 1, :].sum()
1.14764...
Other reductions¶
— works the same way (and take axis=)
Extrema:
>>> x = np.array([1, 3, 2])
>>> x.min()
1
>>> x.max()
3
>>> x.argmin() # index of minimum
0
>>> x.argmax() # index of maximum
1
Logical operations:
>>> np.all([True, True, False])
False
>>> np.any([True, True, False])
True
Note
Can be used for array comparisons:
>>> a = np.zeros((100, 100))
>>> np.any(a != 0)
False
>>> np.all(a == a)
True
>>> a = np.array([1, 2, 3, 2])
>>> b = np.array([2, 2, 3, 2])
>>> c = np.array([6, 4, 4, 5])
>>> ((a <= b) & (b <= c)).all()
True
Statistics:
>>> x = np.array([1, 2, 3, 1])
>>> y = np.array([[1, 2, 3], [5, 6, 1]])
>>> x.mean()
1.75
>>> np.median(x)
1.5
>>> np.median(y, axis=-1) # last axis
array([2., 5.])
>>> x.std() # full population standard dev.
0.82915619758884995
… and many more (best to learn as you go).
Exercise: Reductions
- Given there is a
sum, what other function might you expect to see?- What is the difference between
sumandcumsum?
Worked Example: diffusion using a random walk algorithm

Tip
Let us consider a simple 1D random walk process: at each time step a walker jumps right or left with equal probability.
We are interested in finding the typical distance from the origin of a
random walker after t left or right jumps? We are going to
simulate many “walkers” to find this law, and we are going to do so
using array computing tricks: we are going to create a 2D array with
the “stories” (each walker has a story) in one direction, and the
time in the other:

>>> n_stories = 1000 # number of walkers
>>> t_max = 200 # time during which we follow the walker
We randomly choose all the steps 1 or -1 of the walk:
>>> t = np.arange(t_max)
>>> steps = 2 * np.random.randint(0, 1 + 1, (n_stories, t_max)) - 1 # +1 because the high value is exclusive
>>> np.unique(steps) # Verification: all steps are 1 or -1
array([-1, 1])
We build the walks by summing steps along the time:
>>> positions = np.cumsum(steps, axis=1) # axis = 1: dimension of time
>>> sq_distance = positions**2
We get the mean in the axis of the stories:
>>> mean_sq_distance = np.mean(sq_distance, axis=0)
Plot the results:
>>> plt.figure(figsize=(4, 3))
<Figure size ... with 0 Axes>
>>> plt.plot(t, np.sqrt(mean_sq_distance), 'g.', t, np.sqrt(t), 'y-')
[<matplotlib.lines.Line2D object at ...>, <matplotlib.lines.Line2D object at ...>]
>>> plt.xlabel(r"$t$")
Text(...'$t$')
>>> plt.ylabel(r"$\sqrt{\langle (\delta x)^2 \rangle}$")
Text(...'$\\sqrt{\\langle (\\delta x)^2 \\rangle}$')
>>> plt.tight_layout() # provide sufficient space for labels
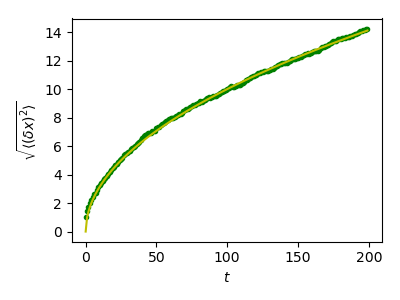
We find a well-known result in physics: the RMS distance grows as the square root of the time!
1.4.2.3. Broadcasting¶
Basic operations on
numpyarrays (addition, etc.) are elementwiseThis works on arrays of the same size.
Nevertheless, It’s also possible to do operations on arrays of differentsizes if NumPy can transform these arrays so that they all havethe same size: this conversion is called broadcasting.
The image below gives an example of broadcasting:
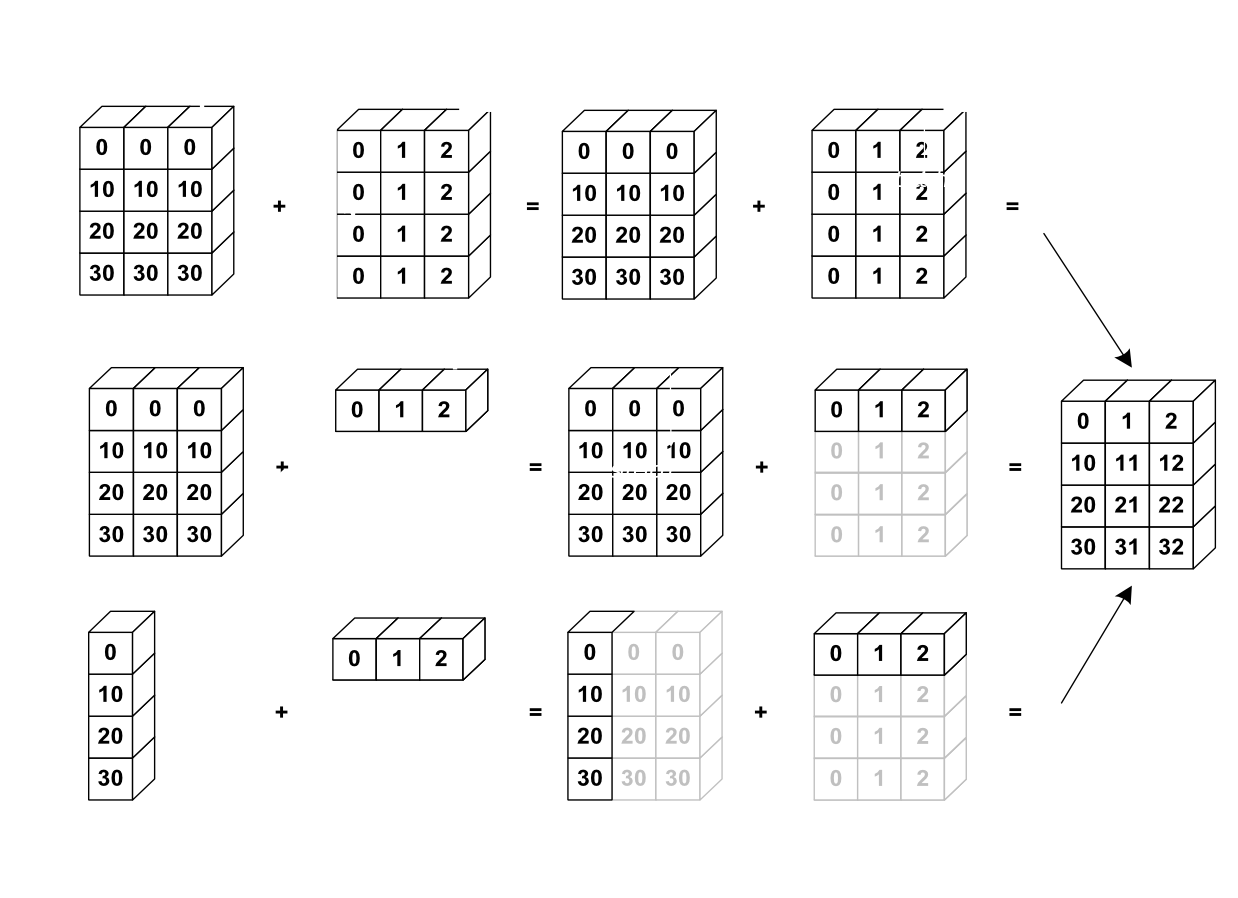
Let’s verify:
>>> a = np.tile(np.arange(0, 40, 10), (3, 1)).T
>>> a
array([[ 0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]])
>>> b = np.array([0, 1, 2])
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
We have already used broadcasting without knowing it!:
>>> a = np.ones((4, 5))
>>> a[0] = 2 # we assign an array of dimension 0 to an array of dimension 1
>>> a
array([[2., 2., 2., 2., 2.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
A useful trick:
>>> a = np.arange(0, 40, 10)
>>> a.shape
(4,)
>>> a = a[:, np.newaxis] # adds a new axis -> 2D array
>>> a.shape
(4, 1)
>>> a
array([[ 0],
[10],
[20],
[30]])
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
Tip
Broadcasting seems a bit magical, but it is actually quite natural to use it when we want to solve a problem whose output data is an array with more dimensions than input data.
Worked Example: Broadcasting
Let’s construct an array of distances (in miles) between cities of Route 66: Chicago, Springfield, Saint-Louis, Tulsa, Oklahoma City, Amarillo, Santa Fe, Albuquerque, Flagstaff and Los Angeles.
>>> mileposts = np.array([0, 198, 303, 736, 871, 1175, 1475, 1544,
... 1913, 2448])
>>> distance_array = np.abs(mileposts - mileposts[:, np.newaxis])
>>> distance_array
array([[ 0, 198, 303, 736, 871, 1175, 1475, 1544, 1913, 2448],
[ 198, 0, 105, 538, 673, 977, 1277, 1346, 1715, 2250],
[ 303, 105, 0, 433, 568, 872, 1172, 1241, 1610, 2145],
[ 736, 538, 433, 0, 135, 439, 739, 808, 1177, 1712],
[ 871, 673, 568, 135, 0, 304, 604, 673, 1042, 1577],
[1175, 977, 872, 439, 304, 0, 300, 369, 738, 1273],
[1475, 1277, 1172, 739, 604, 300, 0, 69, 438, 973],
[1544, 1346, 1241, 808, 673, 369, 69, 0, 369, 904],
[1913, 1715, 1610, 1177, 1042, 738, 438, 369, 0, 535],
[2448, 2250, 2145, 1712, 1577, 1273, 973, 904, 535, 0]])
A lot of grid-based or network-based problems can also use broadcasting. For instance, if we want to compute the distance from the origin of points on a 5x5 grid, we can do
>>> x, y = np.arange(5), np.arange(5)[:, np.newaxis]
>>> distance = np.sqrt(x ** 2 + y ** 2)
>>> distance
array([[0. , 1. , 2. , 3. , 4. ],
[1. , 1.41421356, 2.23606798, 3.16227766, 4.12310563],
[2. , 2.23606798, 2.82842712, 3.60555128, 4.47213595],
[3. , 3.16227766, 3.60555128, 4.24264069, 5. ],
[4. , 4.12310563, 4.47213595, 5. , 5.65685425]])
Or in color:
>>> plt.pcolor(distance)
>>> plt.colorbar()
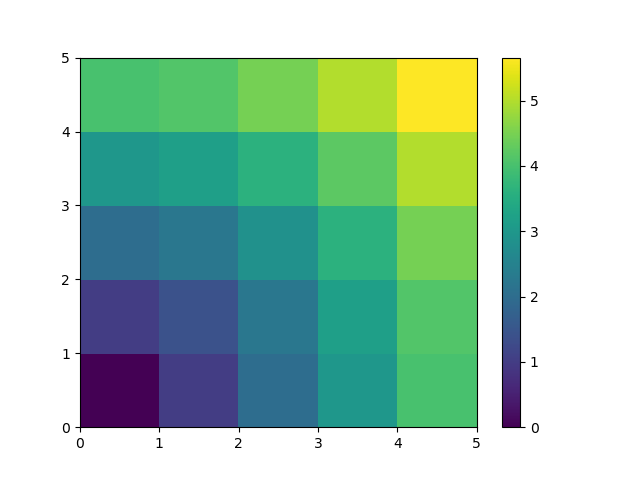
Remark : the numpy.ogrid() function allows to directly create vectors x
and y of the previous example, with two “significant dimensions”:
>>> x, y = np.ogrid[0:5, 0:5]
>>> x, y
(array([[0],
[1],
[2],
[3],
[4]]), array([[0, 1, 2, 3, 4]]))
>>> x.shape, y.shape
((5, 1), (1, 5))
>>> distance = np.sqrt(x ** 2 + y ** 2)
Tip
So, np.ogrid is very useful as soon as we have to handle
computations on a grid. On the other hand, np.mgrid directly
provides matrices full of indices for cases where we can’t (or don’t
want to) benefit from broadcasting:
>>> x, y = np.mgrid[0:4, 0:4]
>>> x
array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
>>> y
array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])
See also
Broadcasting: discussion of broadcasting in the Advanced NumPy chapter.
1.4.2.4. Array shape manipulation¶
Flattening¶
>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> a.ravel()
array([1, 2, 3, 4, 5, 6])
>>> a.T
array([[1, 4],
[2, 5],
[3, 6]])
>>> a.T.ravel()
array([1, 4, 2, 5, 3, 6])
Higher dimensions: last dimensions ravel out “first”.
Reshaping¶
The inverse operation to flattening:
>>> a.shape
(2, 3)
>>> b = a.ravel()
>>> b = b.reshape((2, 3))
>>> b
array([[1, 2, 3],
[4, 5, 6]])
Or,
>>> a.reshape((2, -1)) # unspecified (-1) value is inferred
array([[1, 2, 3],
[4, 5, 6]])
Warning
ndarray.reshape may return a view (cf help(np.reshape))),
or copy
Tip
>>> b[0, 0] = 99
>>> a
array([[99, 2, 3],
[ 4, 5, 6]])
Beware: reshape may also return a copy!:
>>> a = np.zeros((3, 2))
>>> b = a.T.reshape(3*2)
>>> b[0] = 9
>>> a
array([[0., 0.],
[0., 0.],
[0., 0.]])
To understand this you need to learn more about the memory layout of a numpy array.
Adding a dimension¶
Indexing with the np.newaxis object allows us to add an axis to an array
(you have seen this already above in the broadcasting section):
>>> z = np.array([1, 2, 3])
>>> z
array([1, 2, 3])
>>> z[:, np.newaxis]
array([[1],
[2],
[3]])
>>> z[np.newaxis, :]
array([[1, 2, 3]])
Dimension shuffling¶
>>> a = np.arange(4*3*2).reshape(4, 3, 2)
>>> a.shape
(4, 3, 2)
>>> a[0, 2, 1]
5
>>> b = a.transpose(1, 2, 0)
>>> b.shape
(3, 2, 4)
>>> b[2, 1, 0]
5
Also creates a view:
>>> b[2, 1, 0] = -1
>>> a[0, 2, 1]
-1
Resizing¶
Size of an array can be changed with ndarray.resize:
>>> a = np.arange(4)
>>> a.resize((8,))
>>> a
array([0, 1, 2, 3, 0, 0, 0, 0])
However, it must not be referred to somewhere else:
>>> b = a
>>> a.resize((4,))
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: cannot resize an array that has been referenced or is
referencing another array in this way. Use the resize function
Exercise: Shape manipulations
- Look at the docstring for
reshape, especially the notes section which has some more information about copies and views. - Use
flattenas an alternative toravel. What is the difference? (Hint: check which one returns a view and which a copy) - Experiment with
transposefor dimension shuffling.
1.4.2.5. Sorting data¶
Sorting along an axis:
>>> a = np.array([[4, 3, 5], [1, 2, 1]])
>>> b = np.sort(a, axis=1)
>>> b
array([[3, 4, 5],
[1, 1, 2]])
Note
Sorts each row separately!
In-place sort:
>>> a.sort(axis=1)
>>> a
array([[3, 4, 5],
[1, 1, 2]])
Sorting with fancy indexing:
>>> a = np.array([4, 3, 1, 2])
>>> j = np.argsort(a)
>>> j
array([2, 3, 1, 0])
>>> a[j]
array([1, 2, 3, 4])
Finding minima and maxima:
>>> a = np.array([4, 3, 1, 2])
>>> j_max = np.argmax(a)
>>> j_min = np.argmin(a)
>>> j_max, j_min
(0, 2)
Exercise: Sorting
- Try both in-place and out-of-place sorting.
- Try creating arrays with different dtypes and sorting them.
- Use
allorarray_equalto check the results.- Look at
np.random.shufflefor a way to create sortable input quicker.- Combine
ravel,sortandreshape.- Look at the
axiskeyword forsortand rewrite the previous exercise.
1.4.2.6. Summary¶
What do you need to know to get started?
Know how to create arrays :
array,arange,ones,zeros.Know the shape of the array with
array.shape, then use slicing to obtain different views of the array:array[::2], etc. Adjust the shape of the array usingreshapeor flatten it withravel.Obtain a subset of the elements of an array and/or modify their values with masks
>>> a[a < 0] = 0
Know miscellaneous operations on arrays, such as finding the mean or max (
array.max(),array.mean()). No need to retain everything, but have the reflex to search in the documentation (online docs,help(),lookfor())!!For advanced use: master the indexing with arrays of integers, as well as broadcasting. Know more NumPy functions to handle various array operations.
Quick read
If you want to do a first quick pass through the Scipy lectures to learn the ecosystem, you can directly skip to the next chapter: Matplotlib: plotting.
The remainder of this chapter is not necessary to follow the rest of the intro part. But be sure to come back and finish this chapter, as well as to do some more exercices.
